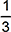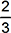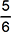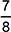Study Guide
Fields 060–063: Elementary Education Generalist
Sample Multiple-Choice Questions
Subtest 2: Mathematics
Objective 0005
Mathematical Computation and Conceptual Skills (Standards 4.1–4.7)
1. Use the table below to answer the question that follows.
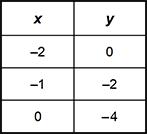
The values in the table represent a linear function. What is the value of the x-intercept of the function?
- 0
- –1
- –2
- –4
- Answer
- Correct Response: C.
This question requires the examinee to demonstrate understanding of functions; algebraic expressions, equations, and inequalities. For any function, including linear functions, the value of the x-intercept is the point where the graph crosses the x-axis. This occurs where y = 0. Therefore, the function crosses, or intercepts, the x-axis at the point having coordinates (–2, 0).
Objective 0005
Mathematical Computation and Conceptual Skills (Standards 4.1–4.7)
2. Use the diagram below to answer the question that follows.
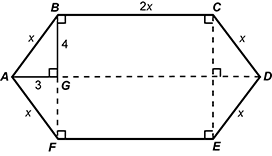
If GB = 4 units and GA = 3 units, what is the area of the hexagon ABCDEF?
- 64 square units
- 104 square units
- 128 square units
- 160 square units
- Answer
- Correct Response: B.
This question requires the examinee to demonstrate understanding of the concepts related to geometric measurement, and tools and techniques used to solve measurement problems. The geometric figure is composed of four right triangles and a rectangle. Using the Pythagorean Theorem (or recognizing a 3-4-5 right triangle) allows the conclusion that x = 5, since 32 + 42 = 25 and 25=52. Then the area can be calculated as the sum of the areas of four 3-4-5 right triangles plus the area of a rectangle with sides 2x = 2(5) = 10 and 4+4 = 8. The area of a right triangle is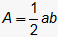 . Each right triangle has an altitude a = 4 and base b = 3. The area of a rectangle is the product of the length and the width. Finding the sum of the areas give 104 square units.
. Each right triangle has an altitude a = 4 and base b = 3. The area of a rectangle is the product of the length and the width. Finding the sum of the areas give 104 square units.
Objective 0005
Mathematical Computation and Conceptual Skills (Standards 4.1–4.7)
3. If a fair coin is tossed 3 times, what is the probability that the coin will land on heads at least once?
- Answer
- Correct Response: D.
This question requires the examinee to demonstrate understanding of methods for determining probabilities. In this situation, it is easiest to first calculate the probability that there are no heads. The only way this happens is by getting a tail on each flip, with a probability of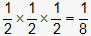 . The probability of at least one head plus the probability of no heads must sum to one, so the probability of at least getting one head must be
. The probability of at least one head plus the probability of no heads must sum to one, so the probability of at least getting one head must be 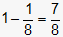 .
.
Objective 0006
Mathematics Literacy and Instruction (Standards 4.8–4.11)
4. Use the diagram below to answer the question that follows.
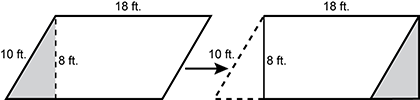
A sixth-grade student finds the area and perimeter of the parallelogram shown above by moving the gray triangle over to the other side and making a rectangle. The student states that the area is 8 × 18 = 144 square feet and the perimeter is 52 feet. For which of the following concepts should the teacher plan instruction to correct the student's misconception?
- Two figures with the same area may not have the same perimeter.
- Figures retain the same area when broken apart and reassembled into a different shape.
- A parallelogram has the same area as a rectangle if both figures have the same base and height.
- The perimeter of a parallelogram is the sum of twice the length of its opposite sides.
- Answer
- Correct Response: A.
This question requires the examinee to demonstrate understanding of methods for planning and delivering evidence-based mathematics instruction. From the evidence given, the student found the area of the parallelogram correctly but calculated the perimeter of the rectangle instead of the original parallelogram. The teacher needs to plan instruction to help the student realize that two figures with the same area do not necessarily have the same perimeter.